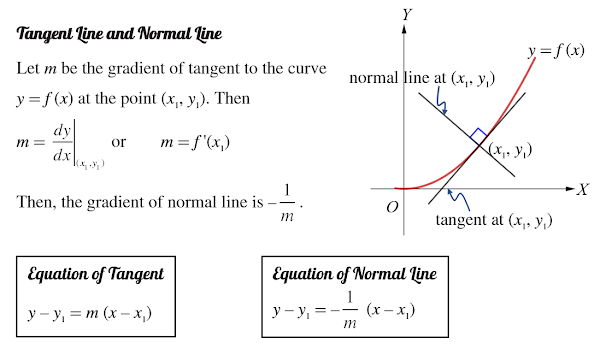
Calculus Exercise (4) : Tangent Line and Normal Line to a Curve
Find the gradient of the curve $y=3 x^{2}-4 x+3$ at the point where $x=2$.
Given that the gradient of the curve $y=x^{2}+a x+b$ at the point $(2,-1)$ is $1$.
Find the values of $a$ and $b$.
Find an equation of the tangent line and normal line to the graph of the function
at the given point.
$\begin{array}{lll}
{} & \textbf{Function} & \textbf{Point}\\\\
\text{(a)} & y=-2 x^{4}+5 x^{2}-3 & (1,0)\\\\
\text{(b)} & y=x^{3}-3 x & (2,2)\\\\
\text{(c)} & y=(x-2)\left(x^{2}+3 x\right)& (1,-4)\\\\
\text{(d)} & y=\dfrac{2}{x^{\frac{3}{4}}} & (1,2)\\
\end{array}$
Find the equations of the tangent and normal lines to the curve $y=3 x^{2}-3 x+2$ at the point where $x=3$.
Find the equation of the tangent to the curve $y=x^{2}+5 x-2$ at the point on the curve where
this curve cuts the line $x=4$.
Find the equations of the tangent and normal lines to the curve $y=x^{2}-5 x+6$ at the points
where this curve cuts the $x$-axis.
$P$ is the point $(3,4)$ on the curve $y=3 x^{2}-12 x+13$. Find the coordinates of the point
of intersection of the normal to the curve at $P$ with the line $x+3=0$.
If the line $2 x+y=3$ is tangent to the curve $y=k x^{2}$, find the value of $k$.
Find an equation of the tangent line to the curve $y=x^{4}+1$ that is parallel to the line $32 x-y=15$.
Find an equation of the normal line to the curve $y=\sqrt{x}$ that is parallel to the line $2 x+y=1$.
Find an equation of the tangent line to the graph of $y=f(x)$ at $x=5$ if $f(5)=-3$ and $f^{\prime}(5)=4$.
solution
$\begin{aligned}
y&=3 x^{2}-4 x+3 \\\\
\frac{d y}{d x}&=6 x-4 \\\\
\left.\frac{d y}{d x}\right|_{x=2}&=6(2)-4\\\\
&=8\\\\
\end{aligned}$
Hence, the gradient of the curve at $x=2$ is 8 .
solution
$\begin{aligned}
y&=x^{2}+a x+b \\\\
\text { At }(2,-1),-1&=(2)^{2}+a(2)+b \\\\
2 a+b&=-5 \\\\
b&=-5-2 a \\\\
\frac{d y}{d x}&=2 x+a\\\\
\left.\frac{d y}{d x}\right|_{(2,-1)}&=4+a\\\\
\left.\frac{d y}{d x}\right|_{(2,-1)}&=1\quad \text { (given) } \\\\
\therefore\ 4+a&=1\\\\
a&=-3 \\\\
\therefore\ b&=-5-2(-3)\\\\&=1
\end{aligned}$
solution
$\begin{aligned}
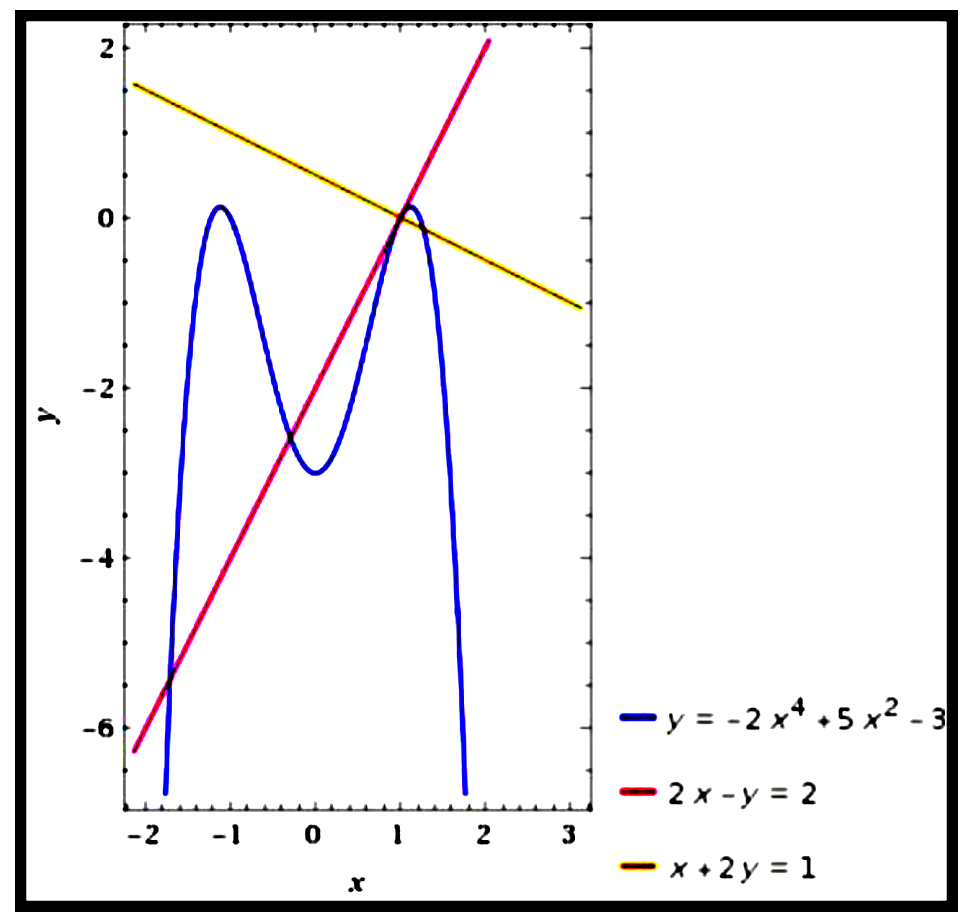
\text{(a)} \quad \text{ Curve}: y&=-2 x^{4}+5 x^{2}-3\\\\
\text{Let} \left(x_{1}, y_{1}\right)&=(1,0)\\\\
\frac{d y}{d x}&=-8 x^{3}+10 x \\\\
\therefore\ m&=\left.\frac{d y}{d x}\right|_{(1,0)}\\\\
&=-8+10\\\\
&=2\\\\
\end{aligned}$
The equation of tangent at $\left(x_{1}, y_{1}\right)$ is $y-y_{1}=m\left(x-x_{1}\right)$
$\begin{aligned}
&\\
\therefore\ y-0&=2(x-1) \\\\
\therefore\ 2 x-y&=2\\\\
\end{aligned}$
The equation of normal at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&=-\frac{1}{m}\left(x-x_{1}\right) \\\\
\therefore\ y-0&=-\frac{1}{2}(x-1) \\\\
\therefore\ x+2 y&=1
\end{aligned}$
$\begin{aligned}
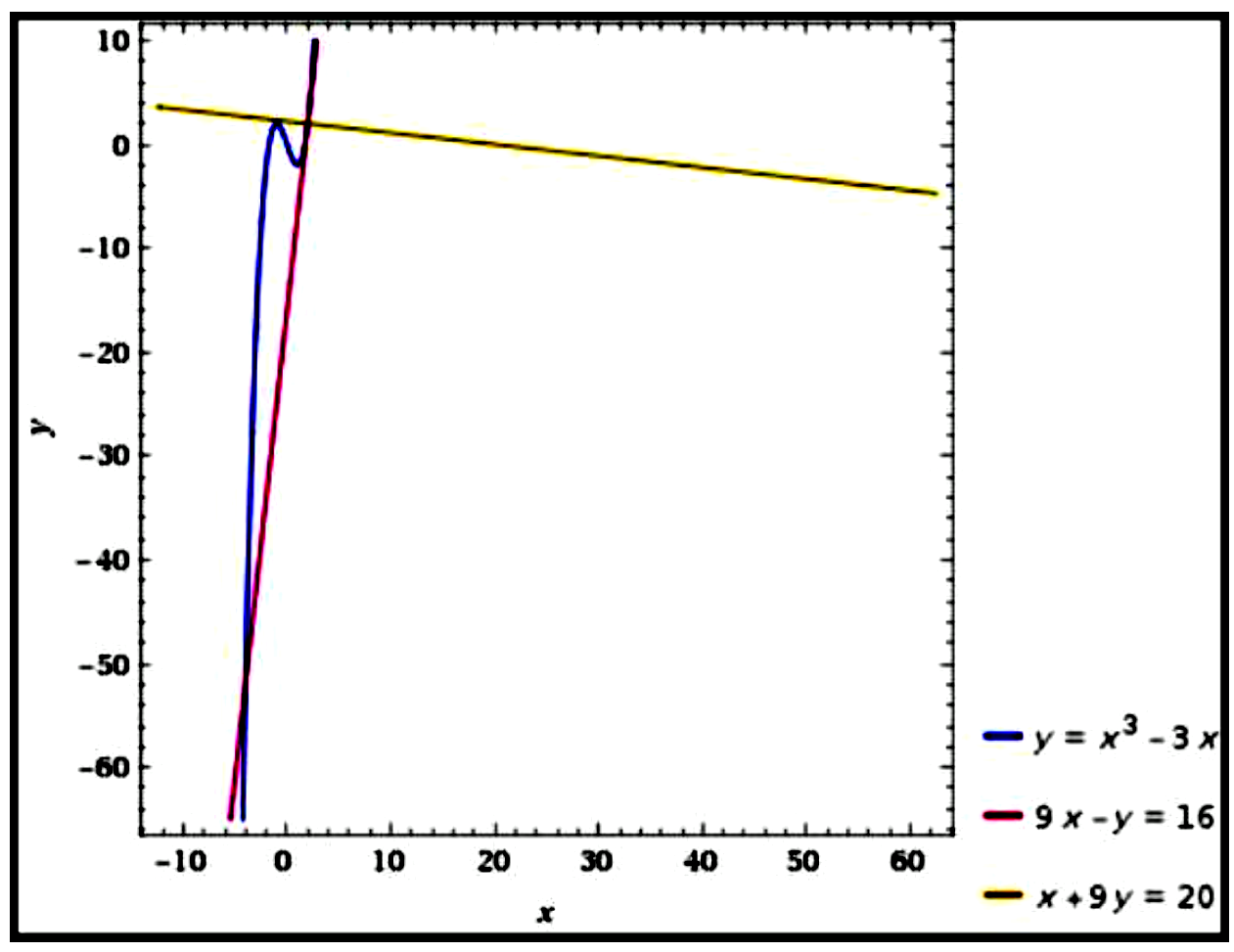
\text{(b)} \quad \text{Curve}: y&=x^{3}-3 x\\\\
\text{Let} \left(x_{1}, y_{1}\right)&=(2,2)
\frac{d y}{d x}&=3 x^{2}-3 \\\\
\therefore\ m&=\left.\frac{d y}{d x}\right|_{(2,2)}&=12-3\\\\
&=9\\\\
\end{aligned}$
The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&=m\left(x-x_{1}\right) \\\\
\therefore\ y-2&=9(x-2) \\\\
\therefore\ 9 x-y&=16\\\\
\end{aligned}$
The equation of normal at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&=-\frac{1}{m}\left(x-x_{1}\right) \\\\
\therefore\ y-2&=-\frac{1}{9}(x-2) \\\\
\therefore\ x+9 y&=20
\end{aligned}$
$\begin{aligned}
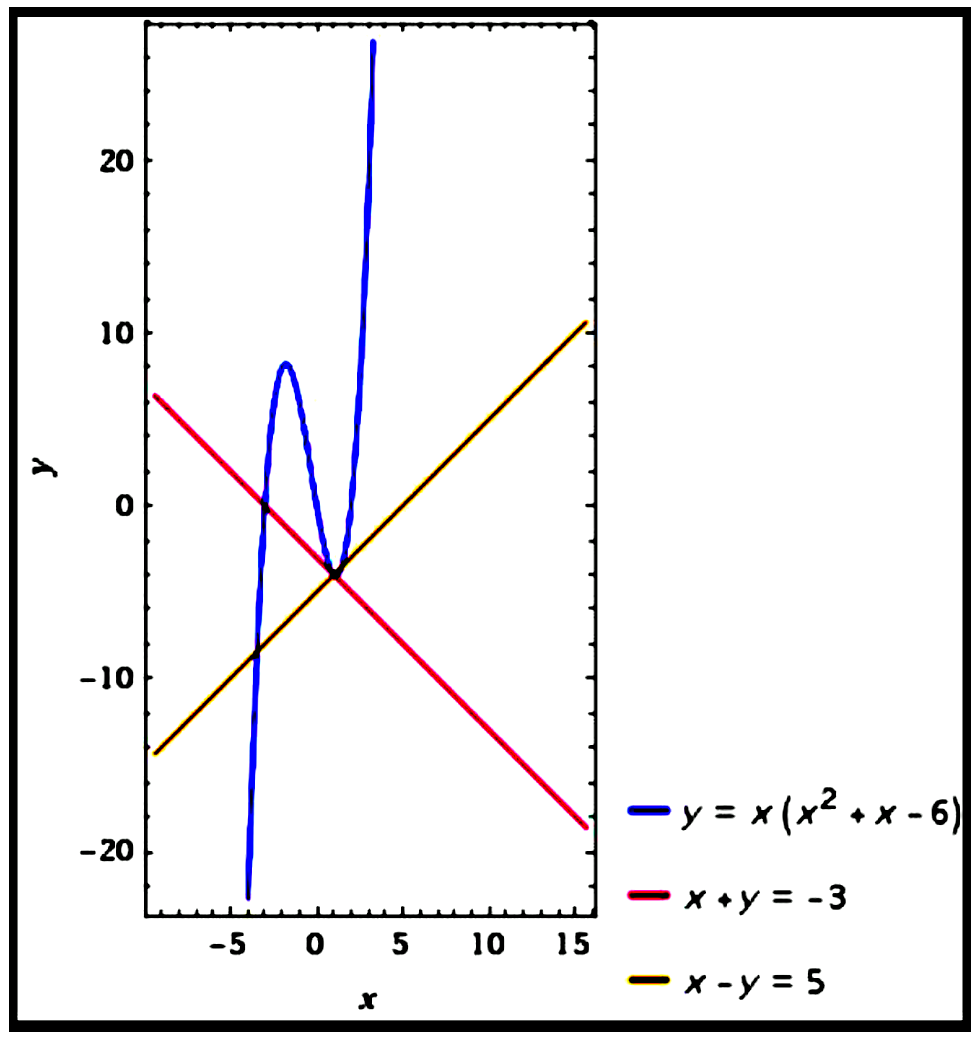
\text {(c)}\quad \text { Curve: } y&=(x-2)\left(x^{2}+3 x\right)&=x^{3}+x^{2}-6 x \\\\
\text { Let }\left(x_{1}, y_{1}\right)&=(1,-4) \\\\
\frac{d y}{d x}&=3 x^{2}+2 x-6 \\\\
\therefore\ m&=\left.\frac{d y}{d x}\right|_{(1,-4)}\\\\
&=3+2-6\\\\
&=-1 \\\\
\end{aligned}$
The equation of tangent at \left(x_{1}, y_{1}\right) is
$\begin{aligned}
&\\
y-y_{1}&=m\left(x-x_{1}\right) \\\\
\therefore\ y+4&=(-1)(x-1) \\\\
\therefore\ x+y&=-3 \\\\
\end{aligned}$
The equation of normal at \left(x_{1}, y_{1}\right) is
$\begin{aligned}
&\\
y-y_{1}&=-\frac{1}{m}\left(x-x_{1}\right) \\\\
\therefore\ y+4&=1(x-1) \\\\
\therefore\ x-y&=5
\end{aligned}$
$\begin{aligned}
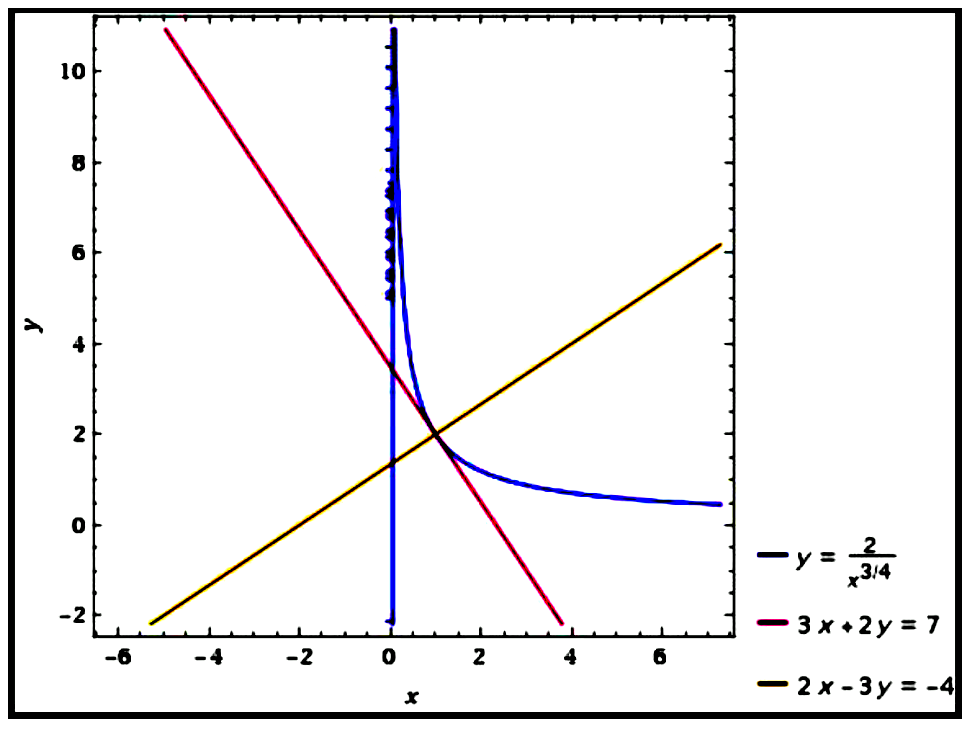
\text {(d)}\quad \text { Curve: } y&=\frac{2}{x^{\frac{3}{4}}} \\\\
\text { Let } \left(x_{1}, y_{1}\right)&=(1,2) \\\\
\frac{d y}{d x}&=-\frac{3}{2 x^{\frac{7}{4}}} \\\\
\therefore\ m&=\left.\frac{d y}{d x}\right|_{(1,2)}\\\\
&=-\frac{3}{2}\\\\
\end{aligned}$
The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&=m\left(x-x_{1}\right) \\\\
\therefore\ y-2&=\left(-\frac{3}{2}\right)(x-1) \\\\
\therefore\ 3 x+2 y&=7
\end{aligned}$
The equation of normal at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&=-\frac{1}{m}\left(x-x_{1}\right) \\\\
\therefore\ y-2&=\frac{2}{3}(x-1) \\\\
\therefore\ 2 x-3 y&=-4
\end{aligned}$
solution
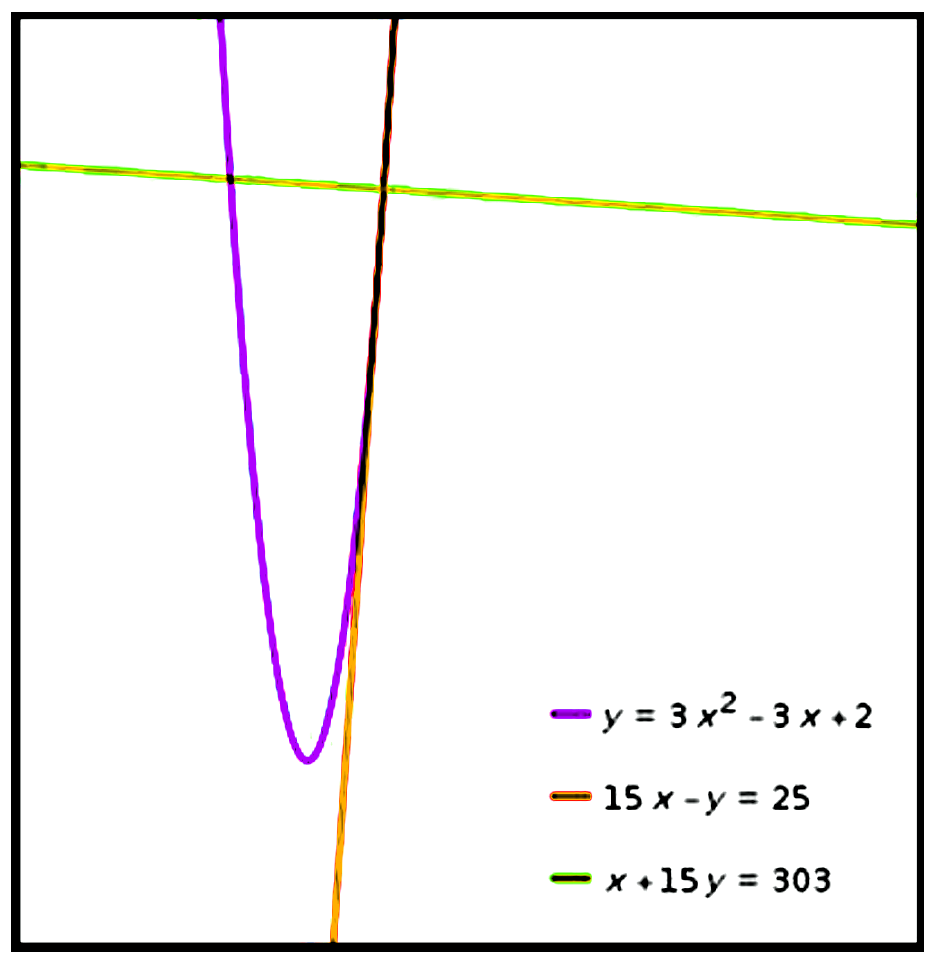
$\begin{aligned}
\text { Curve: } y=3 x^{2}-3 x+2 \\\\
\text { When } x=3, y=3(3)^{2}-3(3)+2=20 \\\\
\text{Let}\left(x_{1}, y_{1}\right)=(3,20) \\\\
\frac{d y}{d x}=6 x-3=3(2 x-1)\\\\
\therefore\ m=\left.\frac{d y}{d x}\right|_{(3,20)}=3(6-1)=15\\\\
\end{aligned}$
The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}=m\left(x-x_{1}\right) \\\\
\therefore\ y-20=15(x-3) \\\\
\therefore\ 15 x-y=25\\\\
\end{aligned}$
The equation of normal at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}=-\frac{1}{m}\left(x-x_{1}\right) \\\\
\therefore\ y-20=-\frac{1}{15}(x-3) \\\\
\therefore\ x+15 y=303
\end{aligned}$
solution
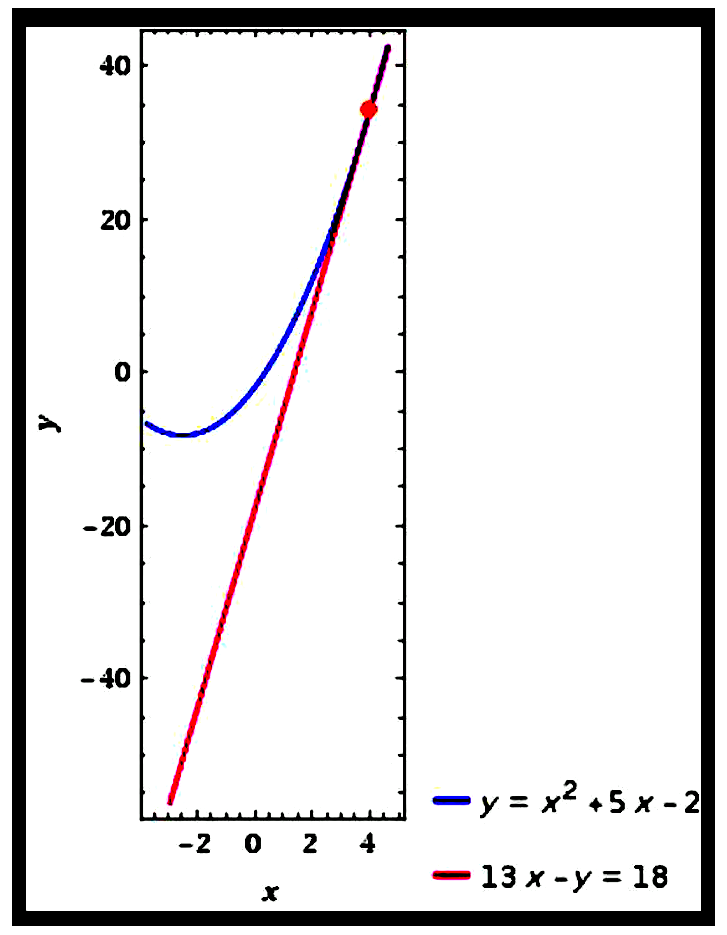
$\begin{aligned}
\text { Curve: } y &=x^{2}+5 x-2 \\\\
\text { When } x &=4, \\\\
y &=(4)^{2}+5(4)-2\\\\
&=34 \\\\
\text{Let} \left(x_{1}, y_{1}\right) &=(4,34) \\\\
\frac{d y}{d x} &=2 x+5\\\\
\therefore m &=\left.\frac{d y}{d x}\right|_{(4,34)}\\\\
&=2(4)+5\\\\
&=13\\\\
\end{aligned}$
The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1} &=m\left(x-x_{1}\right) \\\\
\therefore\ y-34 &=13(x-4) \\\\
\therefore\ 13 x-y &=18
\end{aligned}$
solution
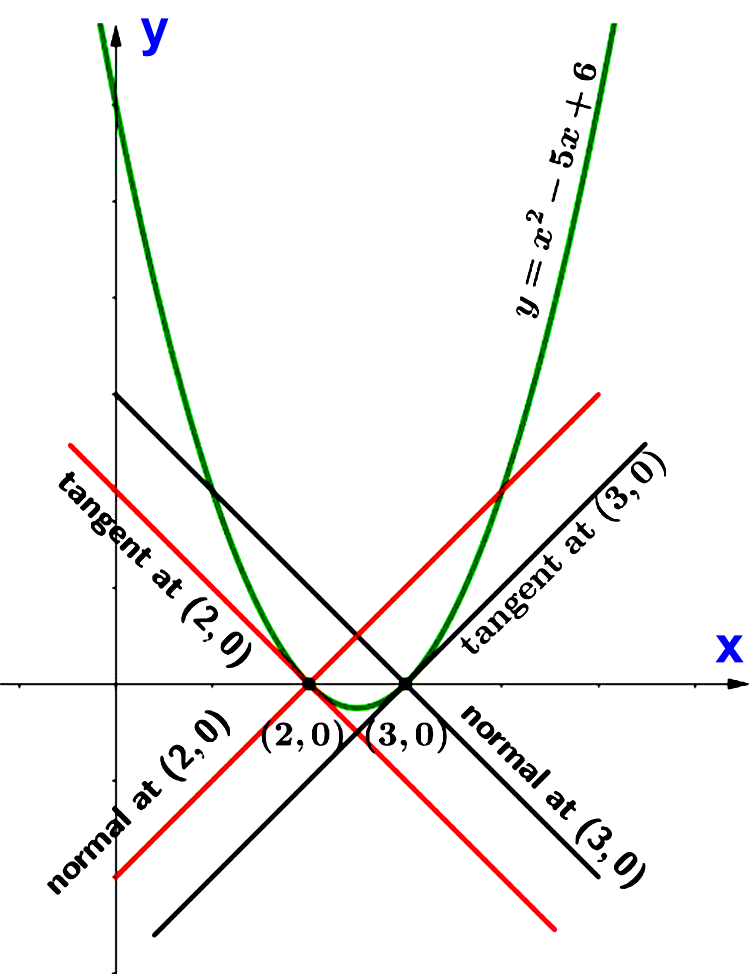
Curve: $y=x^{2}-5 x+6\\\\ $
When this curve cuts the $x$-axis, $y=0$
$\begin{aligned}
&\\
\therefore x^{2}-5 x+6 &=0 \\\\
(x-2)(x-3) &=0 \\\\
x &=2 \text { or } x &=3\\\\
\end{aligned}$
Therefore, the curve cuts the $x$-axis at $(2,0)$ and $(3,0)\\\\ $.
Let $\left(x_{1}, y_{1}\right) =(2,0)$ and $\left(x_{2}, y_{2}\right)=(3,0) $.
$\begin{aligned}
&\\
\therefore\ \frac{d y}{d x} &=2 x-5\\\\
\end{aligned}$
Let the gradient of the curve at $(2,0)$ and $(3,0)$ be $m_{1}$ and $m_{2}$ respectively.
$\begin{aligned}
&\\
\therefore m_{1} &=\left.\frac{d y}{d x}\right|_{(2,0)} &=2(2)-5 &=-1 \\\\
\therefore m_{2} &=\left.\frac{d y}{d x}\right|_{(3,0)} &=2(3)-5 &=1\\\\
\end{aligned}$
$\therefore$ The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1} &=m_{1}\left(x-x_{1}\right) \\\\
y-0 &=-1(x-2) \\\\
y &=2-x\\\\
\end{aligned}$
The equation of normal line at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1} &=-\frac{1}{m_{1}}\left(x-x_{1}\right) \\\\
y-0 &=1(x-2) \\\\
y &=x-2\\\\
\end{aligned}$
The equation of tangent at $\left(x_{2}, y_{2}\right)$ is
$\begin{aligned}
&\\
y-y_{2} &=m_{2}\left(x-x_{2}\right) \\\\
y-0 &=1(x-3) \Rightarrow y &=x-3\\\\
\end{aligned}$
The equation of normal line at $\left(x_{2}, y_{2}\right)$ is
$\begin{aligned}
& \\
y-y_{2} &=-\frac{1}{m_{2}}\left(x-x_{2}\right) \\\\
y-0 &=-1(x-3) \\\\
y &=3-x
\end{aligned}$
solution
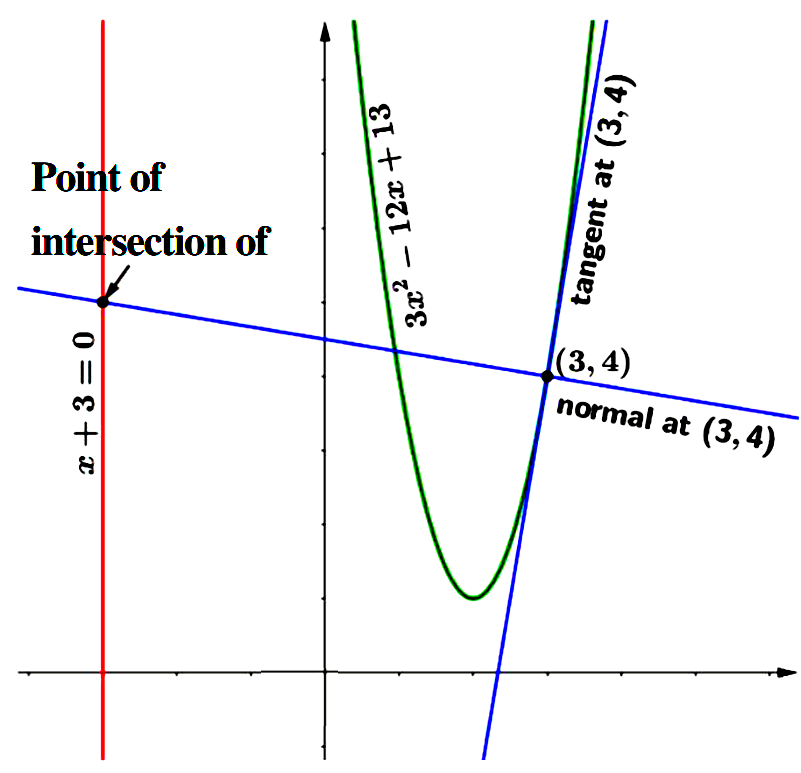
Curve: $y=3 x^{2}-12 x+13\\\\ $,
Line: $x+3=0 \Rightarrow x=-3\\\\ $
$P(3,4)$ is on the curve.
Let $\left(x_{1}, y_{1}\right)=(3,4)\\\\ $.
$\therefore\ \dfrac{d y}{d x}=6 x-12=6(x-2)\\\\ $
$\therefore\ m=\left.\dfrac{d y}{d x}\right|_{(3,4)}=6(3-2)=6\\\\ $
The equation of normal line at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&=-\frac{1}{m}\left(x-x_{1}\right) \\\\
y-4&=-\frac{1}{6}(x-3) \\\\
y&=-\frac{1}{6}(x-3)+4\\\\
\end{aligned}$
When this normal line intersects the line $x+3=0$, $x=-3$.
$\begin{aligned}
&\\
\therefore\ y&=-\frac{1}{6}(-3-3)+4\\\\
&=5\\\\
\end{aligned}$
So, the point of intersection of the normal to the curve at $P(3,4)$ with the line $x+3=0$ is $(-3,5)$.
solution
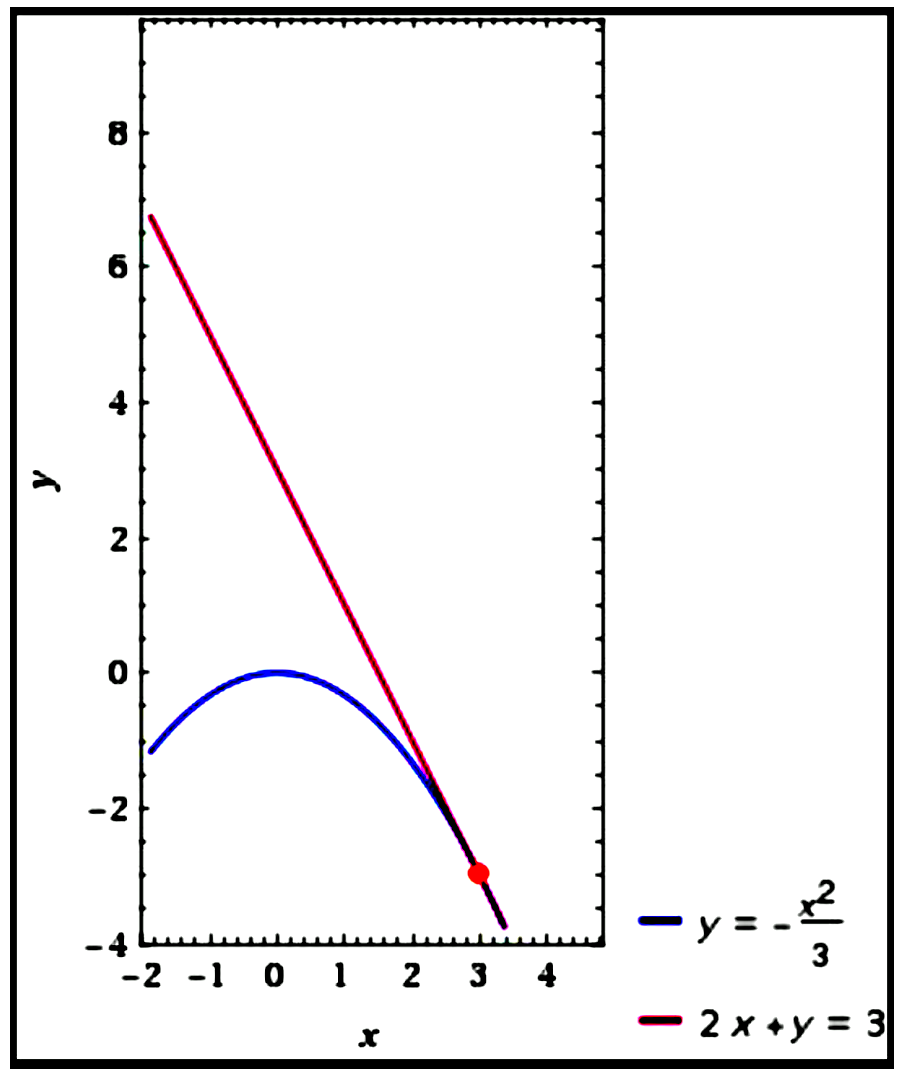
$\begin{aligned}
\text{Curve }: y&=k x^{2},\\\\
\therefore\ \text{ Gradient of tangent } &=\frac{d y}{d x}\\\\
&=2 k x\\\\
\text{Tangent }: 2 x+y&=3 \\\\
y&=-2 x+3\\\\
\therefore\ \text{ Gradient of tangent } &=-2\\\\
\therefore\ 2 k x&=-2 \\\\
x&=-\frac{1}{k}\\\\
\end{aligned}$
Substituting $x=-\dfrac{1}{k}$ in curve and line equations,
$\begin{aligned}
&\\
y&=k\left(-\frac{1}{k}\right)^{2} \\\\
y&=\frac{1}{k} \\\\
\therefore\ \frac{1}{k}&=-2\left(-\frac{1}{k}\right)+3\\\\
k&=-\frac{1}{3}
\end{aligned}$
solution
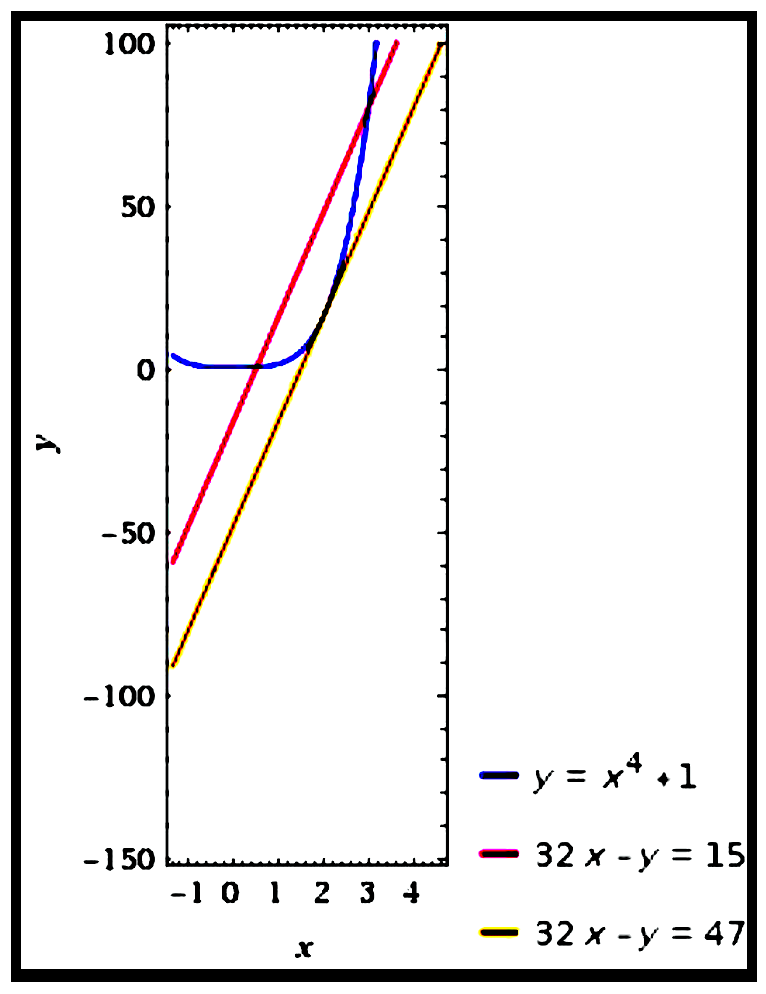
$\begin{aligned}
\text { Curve: } y &=x^{4}+1 \\\\
\therefore \text { Gradient of tangent } &=\frac{d y}{d x} \\\\
&=4 x^{3} \\\\
\text { Line: } 32 x-y &=15 \\\\
y &=32 x-15 \\\\
\therefore\ \text { Gradient of line } &=32 \\\\
\end{aligned}$
Since the tangent line to the curve is parallel to the line $32 x-y$,
$\begin{aligned}
&\\
4 x^{3} &=32 \\\\
x &=2 \\\\
\text { When } x &=2, \\\\
y &=(2)^{4}+1 \\\\
&=17 \\\\
\text { Let }\left(x_{1}, y_{1}\right) &=(2,17). \\\\
\therefore\ \text { The equation of tangent at } & \left(x_{1}, y_{1}\right) \text { is } \\\\
y-y_{1} &=m\left(x-x_{1}\right) \\\\
\therefore\ y-17 &=32(x-2) \\\\
\therefore\ 32 x-y &=47
\end{aligned}$
solution
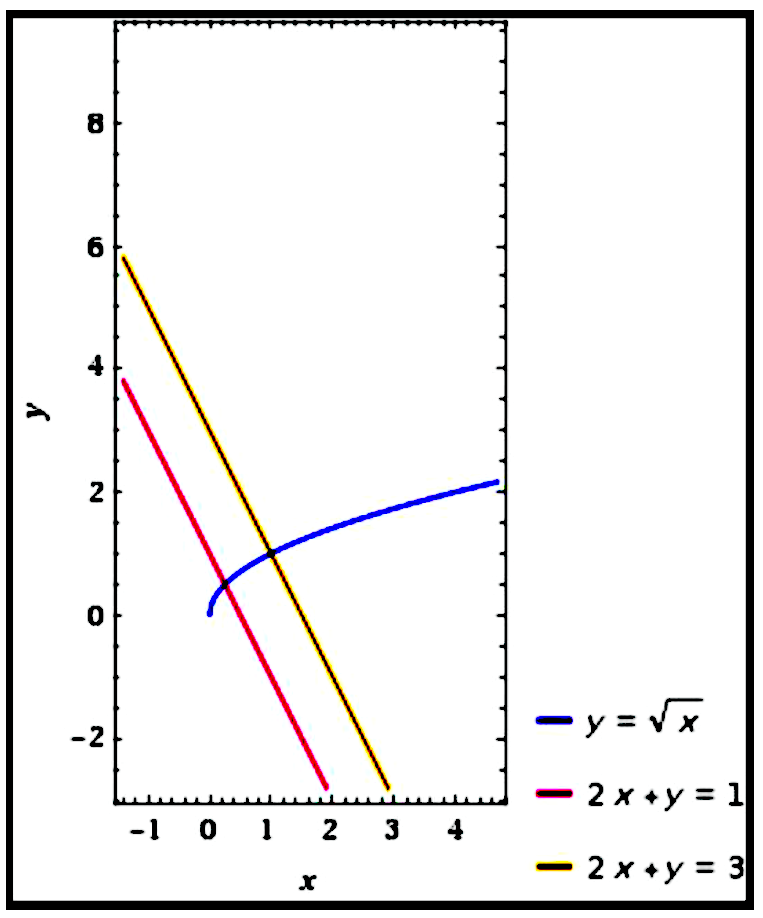
$\begin{aligned}
\text { Curve: } y &=\sqrt{x} \\\\
\therefore \text { Gradient of tangent } &=\frac{d y}{d x} \\\\
&=\frac{1}{2 \sqrt{x}} \\\\
\therefore \text { Gradient of normal } &=-2 \sqrt{x} \\\\
\text { Line }: 2 x+y &=1 \\\\
\qquad y &=-2 x+1 \\\\
\therefore \text { Gradient of line } &=-2 \\\\
\end{aligned}$
Since the normal line to the curve is parallel to the line $2 x+y =1$.
$\begin{aligned}
&\\
-2 \sqrt{x}=-2 & \\\\
\qquad x=1 & & \\\\
\text { When } x=1, y=\sqrt{1}=1\\\\
\text { Let } \left(x_{1}, y_{1}\right)=(1,1)\\\\
\end{aligned}$
$\therefore$ The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-1&=-2(x-1) \\\\
2 x+y&=3
\end{aligned}$
solution
If the tangent line to the curve $y=f(x)$ at $(4,3)$ cuts the $y$ - axis at $(0,2)$, find $f(4)$
and $f^{\prime}(4)$.
solution
The tangent line to the curve $y=f(x)$ at $(4,3)$ cuts the $y$-axis at $(0,2)$.
$\begin{aligned}
&\\
\therefore\ f(4)&=3\\\\
\therefore\ f^{\prime}(4)&= \text{ gradient of tangent}\\\\
&=\frac{3-2}{4-0} \\\\
&=\frac{1}{4}
\end{aligned}$
If the tangent lines to the curve $y=4 x^{2}-x^{3}$ at the points where $x=-1$ and $x=2$ intersect
at $P$, find the coordinates of the point $P$.
solution
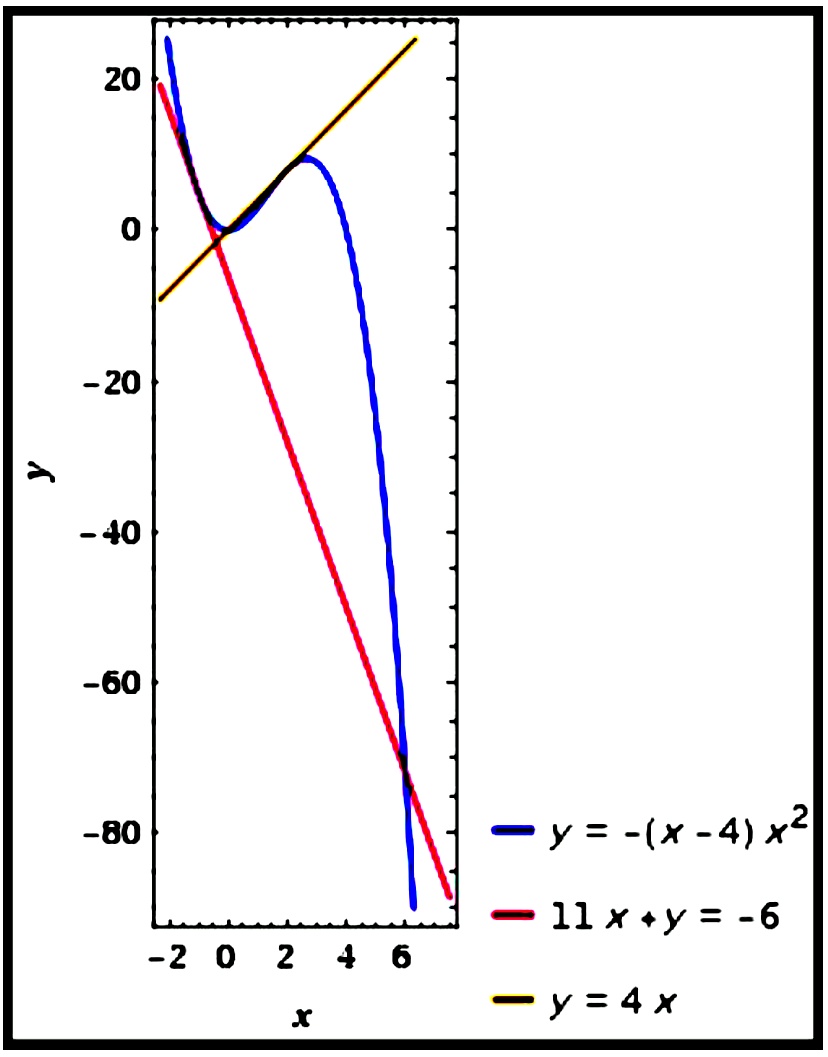
$\begin{aligned}
\text{Curve }: y&=4 x^{2}-x^{3}\\\\
\text{When } x&=-1,\\\\
y &=4(-1)^{2}-(-1)^{3} \\\\
&=5\\\\
\text{When } x&=2,\\\\
y &=4(2)^{2}-(2)^{3} \\\\
&=8\\\\
\end{aligned}$
Let $\left(x_{1}, y_{1}\right)=(-1,5)$ and $\left(x_{2}, y_{2}\right)=(2,8)$.
$\begin{aligned}
&\\
\dfrac{d y}{d x}=8 x-3 x^{2}\\\\
\end{aligned}$
Let the gradient of tangents at $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$ be $m_{1}$ and $m_{2}$ respectively.
$\begin{aligned}
&\\
\therefore\ m_{1} &=\left.\dfrac{d y}{d x}\right|_{(-1,5)} \\\\
&=8(-1)-3(-1)^{2} \\\\
&=-11 \\\\
m_{2} &=\left.\dfrac{d y}{d x}\right|_{(2,8)} \\\\
&=8(2)-3(2)^{2} \\\\
&=4\\\\
\end{aligned}$
Let the point of intersection of two tangents be $(a, b)$.
$\begin{aligned}
&\\
\dfrac{b-5}{a+1} &=-11 \\\\
11 a+b &=-6 \\\\
\dfrac{b-8}{a-2} &=4 \\\\
4 a-b &=0\\\\
\end{aligned}$
Solving equations (1) and (2) yields $a=-\dfrac{2}{5}$ and $b=-\dfrac{8}{5}$
$\begin{aligned}
&\\
\therefore\ P=\left(-\dfrac{2}{5},-\dfrac{8}{5}\right) .
\end{aligned}$
Find the coordinates of point or points on the curve $y=x^{4}-2 x^{2}+3$ at which the curve has
horizontal tangent(s).
solution
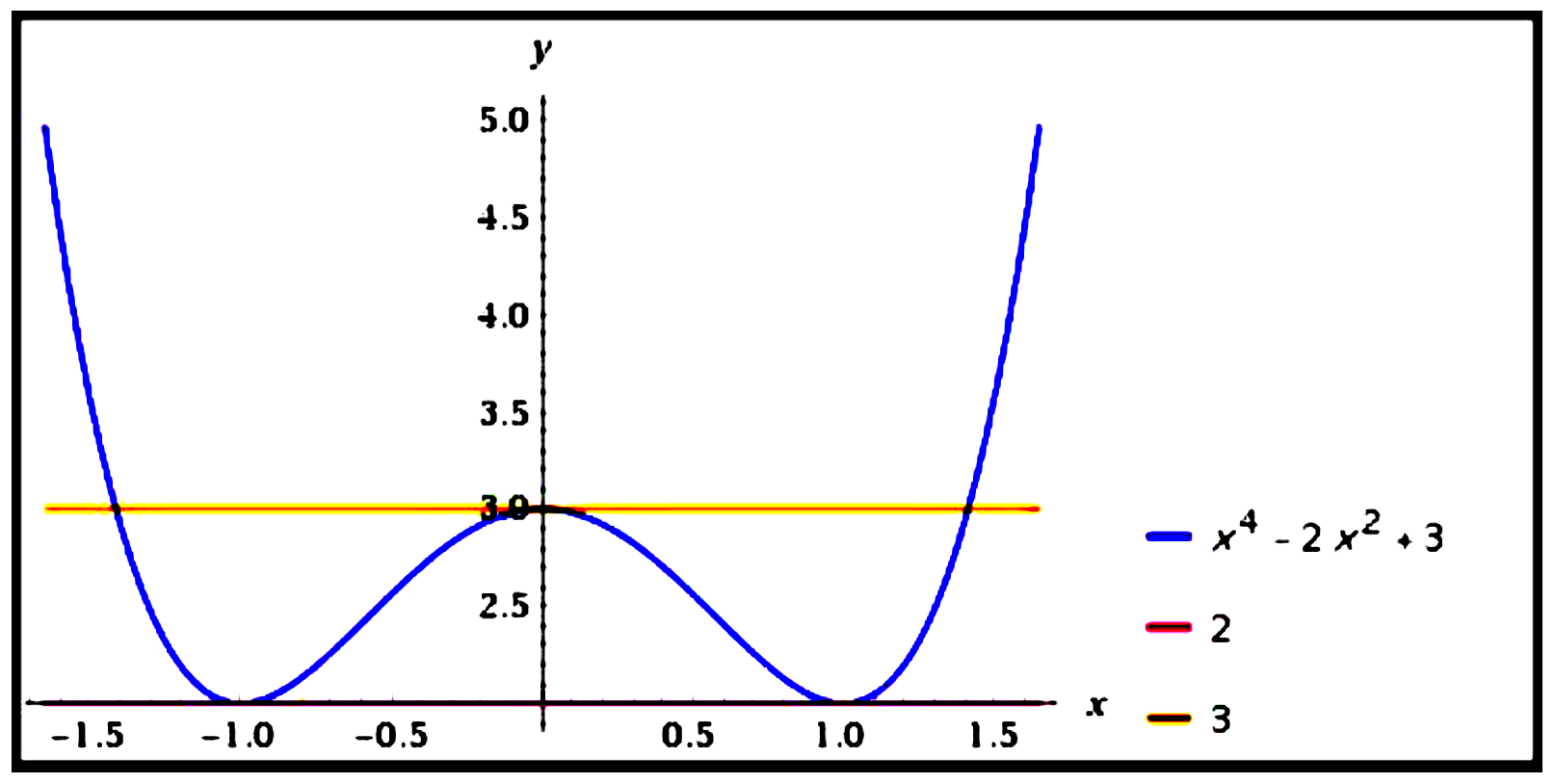
$\begin{aligned}
\text{Curve }: y&=x^{4}-2 x^{2}+3\\\\
\frac{d y}{d x} &=4 x^{3}-4 x \\\\
&=4 x\left(x^{2}-1\right) \\\\
&=4 x(x+1)(x-1)\\\\
\end{aligned}$
For horizontal tangents,
$\begin{aligned}
&\\
\frac{d y}{d x} &=0 . \\\\
4 x(x+1)(x-1) &=0 \\\\
\therefore x=-1 \text { or } x &=0 \text { or } x=1 . \\\\
x=-1 \Rightarrow y &=(-1)^{4}-2(-1)^{2}+3=2 \\\\
x=0 \Rightarrow y &=(0)^{4}-2(0)^{2}+3=3 \\\\
x=1 \Rightarrow y &=(1)^{4}-2(1)^{2}+3=2\\\\
\end{aligned}$
The points on the curve $y=x^{4}-2 x^{2}+3$ at which the curve
has horizontal tangents are $(-1,2),(0,3)$ and $(1,2)$.
The curve $y=x^{3}+a x^{2}+b x+c$, where $a, b$ and $c$ are real constants, touches the $x$-axis at
$x=1$ and cuts the $x$-axis at $x=4$. Find (i) the values of $a, b$ and $c$, (ii) the equation of the
tangent to the curve at $x=0$.
solution
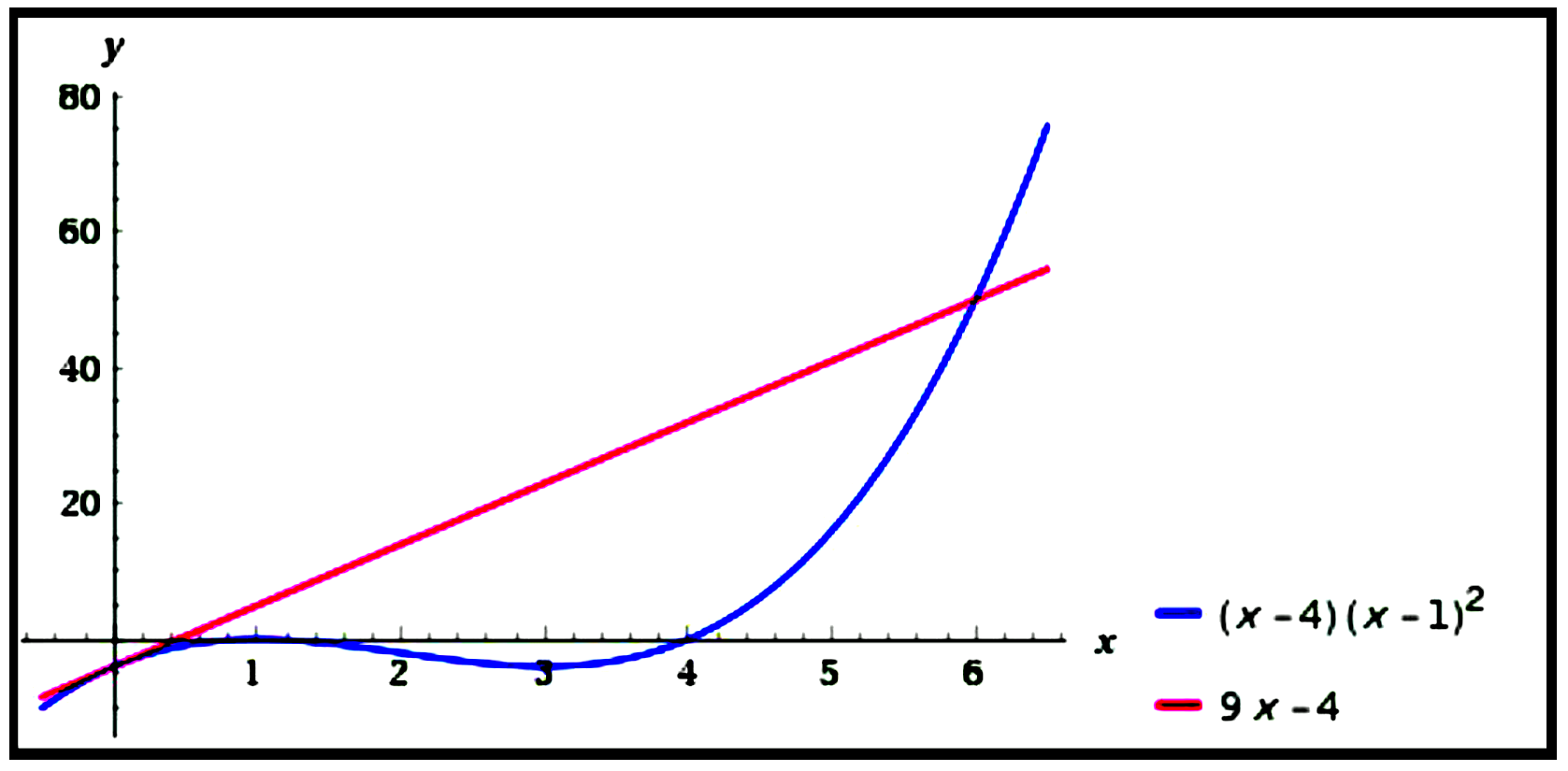
Curve: $y=x^{3}+a x^{2}+b x+c\\\\ $
Since the curve touches the $x$-axis at $x=1$ and cuts the $x$-axis at $x=4$, the points
$(1,0)$ and $(4,0)$ lie on the curve and the gradient of tangent at $(1,0)$ is 0 .
$\begin{aligned}
&\\
\therefore(1)^{3}+a(1)^{2}+b(1)+c &=0 \\\\
a+b+c &=-1 \ldots(1)\\\\
(4)^{3}+a(4)^{2}+b(4)+c &=0 \\\\
16 a+4 b+c &=-64 \ldots(2) \\\\
\text{By equation (2)- equation(1)} & \\\\
15 a+3 b &=-63 \\\\
5 a+b &=-21 \ldots(3)\\\\
\end{aligned}$
The gradient of the tangent at any point $(x, y)$ on the curve is $\frac{d y}{d x}$.
$\begin{aligned}
&\\
\frac{d y}{d x} &=3 x^{2}+2 a x+b \\\\
\left.\frac{d y}{d x}\right|_{(1,0)} &=0 \\\\
3+2 a+b &=0 \\\\
2 a+b &=-3 \ldots(4)\\\\
\text{By equation (3)- equation(4)} & \\\\
3 a &=-18 \\\\
a &=-6 \\\\
\text { Substituting } a &=-6 \text { in (4), } \\\\
-12+b &=-3 \\\\
b &=9 \\\\
\text { Substituting } a &=-6 \text { and } b=9 \text { in (1), } \\\\
-6+9+c &=-1 \\\\
c &=-4 \\\\
\therefore\ y &=x^{3}-6 x^{2}+9 x-4.\\\\
\end{aligned}$
Substituting $a=-6$ and $b=9$ in (1),
When $x=0, y=-4\\\\ $
Hence $(0,-4)$ lies on the curve.
$\therefore$ The gradient of the tangent at $(0,-4)$ on the curve is
$\begin{aligned}
&\\
\left.\frac{d y}{d x}\right|_{(0,-4)}& =b=9 \\\\
\therefore\ \text { The equation of tangent at } & (0,-4) \text { is } \\\\
y-(-4) &=9(x-0) \\\\
y &=9 x-4 .
\end{aligned}$
Find all values of $m$ such that the line $y=m x+3$ is tangent to the curve $y=\frac{1}{2} x^{2}-x+5$.
solution
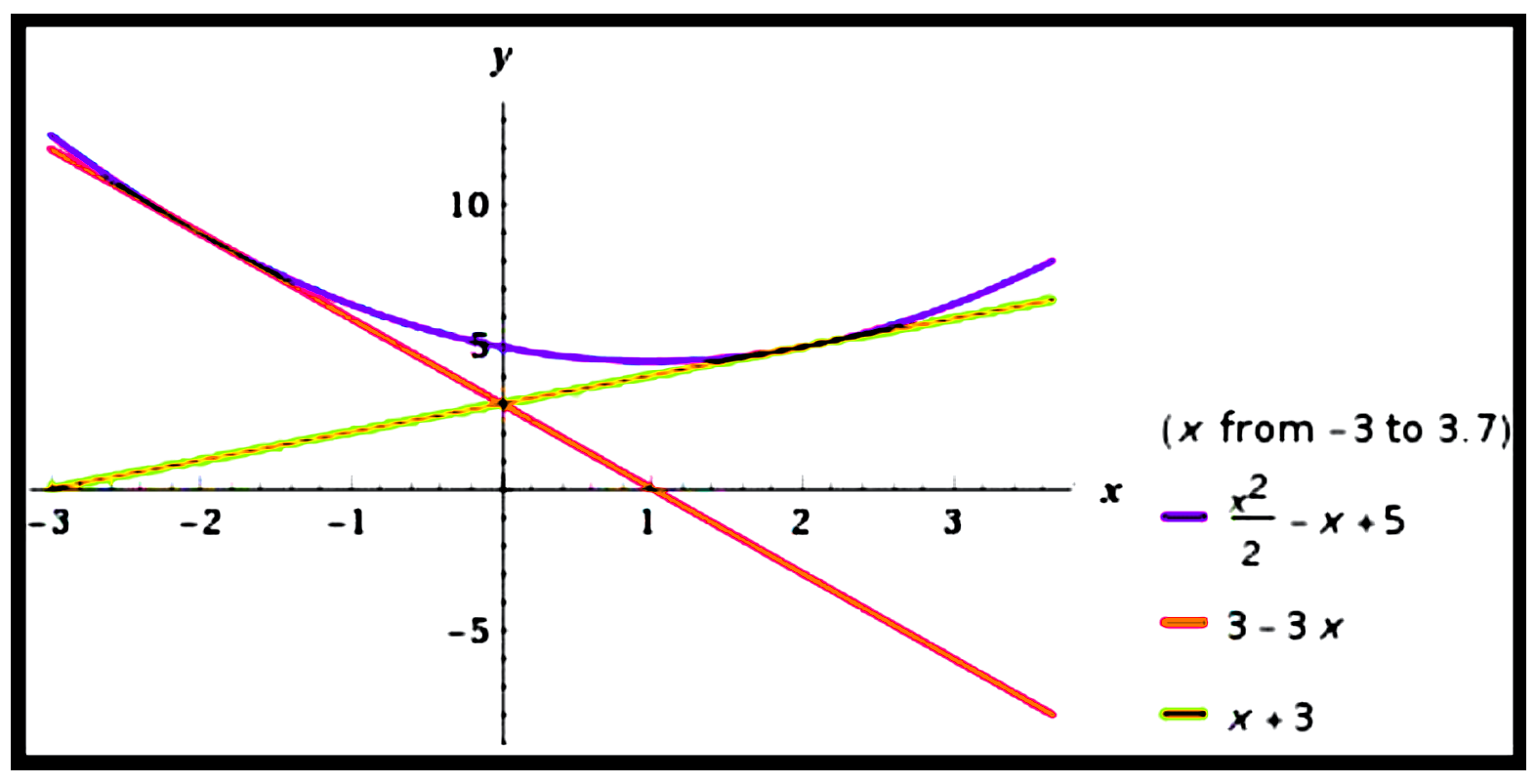
$\begin{aligned}
\text{ Curve }: y &= \frac{1}{2} x^{2}-x+5.\\\\
\text{ Gradient of tangent is } \frac{d y}{d x} &= x-1\\\\
\text{ Tangent }: y &= m x+3\\\\
\text{ Gradient of tangent } &= m\\\\
\therefore\ m &= x-1\\\\
x &= m+1\\\\
\text{Substituting } x &= m+1 \text{ in curve equation},\\\\
y &= \frac{1}{2}(m+1)^{2}-(m+1)+5\\\\
\text{Substituting } x &= m+1 \text{ in tangent equation}\\\\
y &= m(m+1)+3\\\\
\therefore\ \frac{1}{2}(m+1)^{2}-(m+1)+5 &= m(m+1)+3\\\\
m = -3 \text{ or } m &= 1
\end{aligned}$
If the tangent to the curve $y=2 x^{3}-3 x+5$ at the point where $x=-1$ intersects the curve again at $A$,
find the coordinates of $A$.
solution
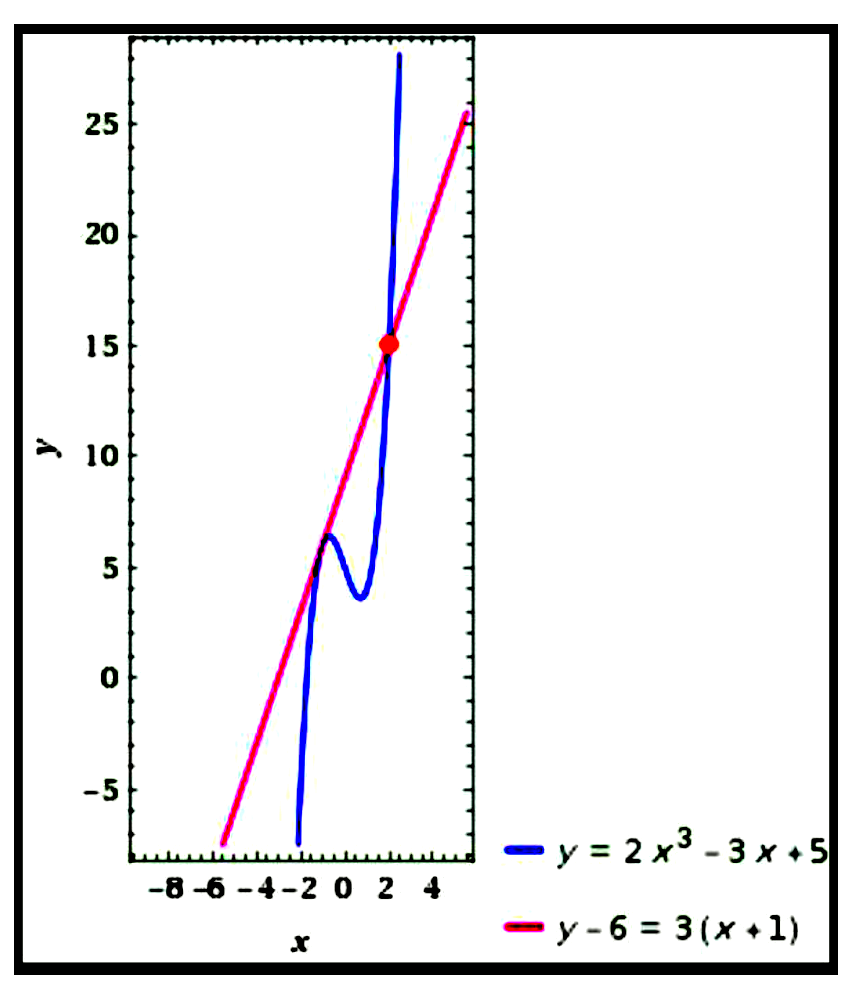
$\begin{aligned}
\text{ Curve }: y &= 2 x^{3}-3 x+5\\\\
\text{ When} x &= -1,\\\\
y &= 2(-1)^{3}-3(-1)+5 &= 6\\\\
\frac{d y}{d x} &= 6 x^{2}-3\\\\
&= 3\left(2 x^{2}-1\right)\\\\
m &= \left.\frac{d y}{d x}\right|_{(-1,6)}\\\\
&= 3\\\\
\end{aligned}$
Let another point of intersection of curve and tangent be $(a, b)$.
$\begin{aligned}
&\\
\therefore b &= 2 a^{3}-3 a+5\\\\
\text{Since, } \frac{b-6}{a+1} &= 3\\\\
\frac{2 a^{3}-3 a+5-6}{a+1} &= 3\\\\
a &= 2\\\\
\therefore b &= 2(2)^{3}-3(2)+5\\\\
&= 15\\\\
\end{aligned}$
Thus, the coordinates of the point $A $ is $(2,15)$.
If the lines passing through the point $(2,3)$ are tangent to the curve $y=3 x-x^{2}$, find the coordinates
of the points on the curve where the tangents meet the curve.
solution
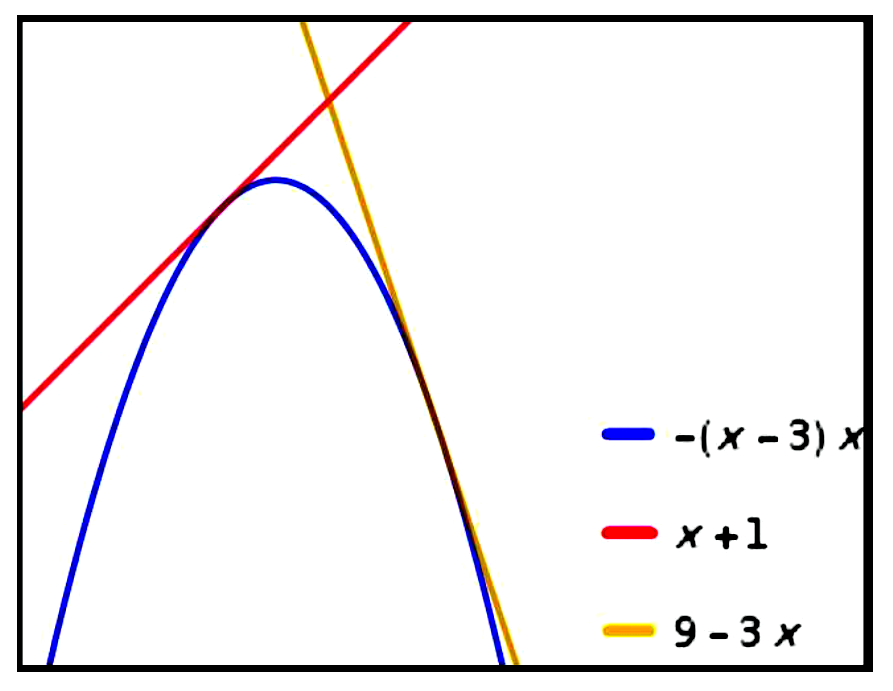
$\begin{aligned}
&\text { Curve: } y=3 x-x^{2} \\\\
&\frac{d y}{d x}=3-2 x \\\\
&\text { Let }(a, b) \text { be the point on the curve } \\\\
&\text { where the tangent exists. } \\\\
&\therefore b=3 a-a^{2} \\\\
&m=\left.\frac{d y}{d x}\right|_{(a, b)}=3-2 a \\\\
&\text { Since the tangent at }(a, b) \text { pass } \\\\
&\text { through the point } (2,3), \\\\
&\frac{b-3}{a-2}=3-2 a \\\\
&\frac{3 a-a^{2}-3}{a-2}=3-2 a \\\\
&\therefore a=1(\text { or }) a=3 \\\\
&\text { When } a=1, b=3(1)-(1)^{2}=2 \\\\
&\text { When } a=3, b=3(3)-(3)^{2}=0 \\\\
&\therefore \text { The tangents meet the curve at }(1,2) \\\\
&\text { and }(3,0) \text {. }
\end{aligned}$

Posting Komentar untuk "Calculus Exercise (4) : Tangent Line and Normal Line to a Curve"