Calculus Exercise (5) : Change Rule, Product Rule and Quotient Rule
Differentiate the following with respect to $x$.
(a) $\left(2 x^{2}+3 x\right)^{10}\\\\ $
(b) $\dfrac{1}{3-2 x}\\\\ $
(c) $\sqrt{9-x^{2}}\\\\ $
(d) $\left(x^{2}+\dfrac{3}{x}\right)^{5}\\\\ $
Differentiate $\sqrt{x+7}\left(x^{2}+2\right)^{7}$ with respect to $x$.
Differentiate $\dfrac{x^{2}}{\sqrt{x+1}}$ with respect to $x$.
Differentiate the following with respect to $x.\\\\ $
(a) $\left(2 x^{2}+3\right)^{4}\left(x^{2}-3 x\right)^{5}\\\\ $
(b) $\left(3+x^{2}\right) \sqrt{3-x^{2}}\\\\ $
(c) $\dfrac{\sqrt{x+3}}{x+1}\\\\ $
(d) $\dfrac{3 x-5}{2 x^{2}+7}\\\\ $
(e) $\dfrac{2 x-7}{\sqrt{x+7}}\\\\ $
(f) $\sqrt{\dfrac{x^{2}+1}{x^{2}-1}}\\\\ $
Calculate the gradient of the curve $y=\dfrac{3 x^{2}-8}{5-2 x}$ at the point $(2,4)$.
Calculate the gradient of the curve $y=x \sqrt{x+3}$.
Find the coordinate of the point at which the gradient is zero.
Find the equation of the normal to the curve $y=\dfrac{x^{2}+1}{x-1}$ at the point
on the curve where $x=2$.
Find the equation of the normal to the curve $y=\dfrac{4 x+1}{x-1}$ at the point
on the curve where $y=5$.
If $f(x)=\dfrac{k+x}{1-2 x}$ where $k$ is a constant, find $f^{\prime}(x)$ in terms of
$x$ and $k$. Given that $f^{\prime}(3)=0.52$, show that $k=6$.
Find the equation of the normal to the curve $y=6-(x-2)^{4}$ at the point on the curve
where $x=1$.
The tangent to the curve $y=\left(\dfrac{x}{2}-1\right)^{6}$, at the point
where $x=4$, meets the $y$-axis at $A$. Find the coordinates of $A$.
Show that the tangent to the curve $y=(x+2 a)^{3}$ at the point where $y=a^{3}$
is $y=3 a^{2} x+4 a^{3} .$
Find equations of the tangent lines to the curve $y=\dfrac{x+1}{x-1}$ that are
parallel to the line $2 y+x=6$.
The equation of a curve is $y=\dfrac{x^{2}+6}{x-3}$.
Find the gradient of tangent to the curve at the point $x=4$.
Hence, find the equation of the normal to the curve at $x=4$.
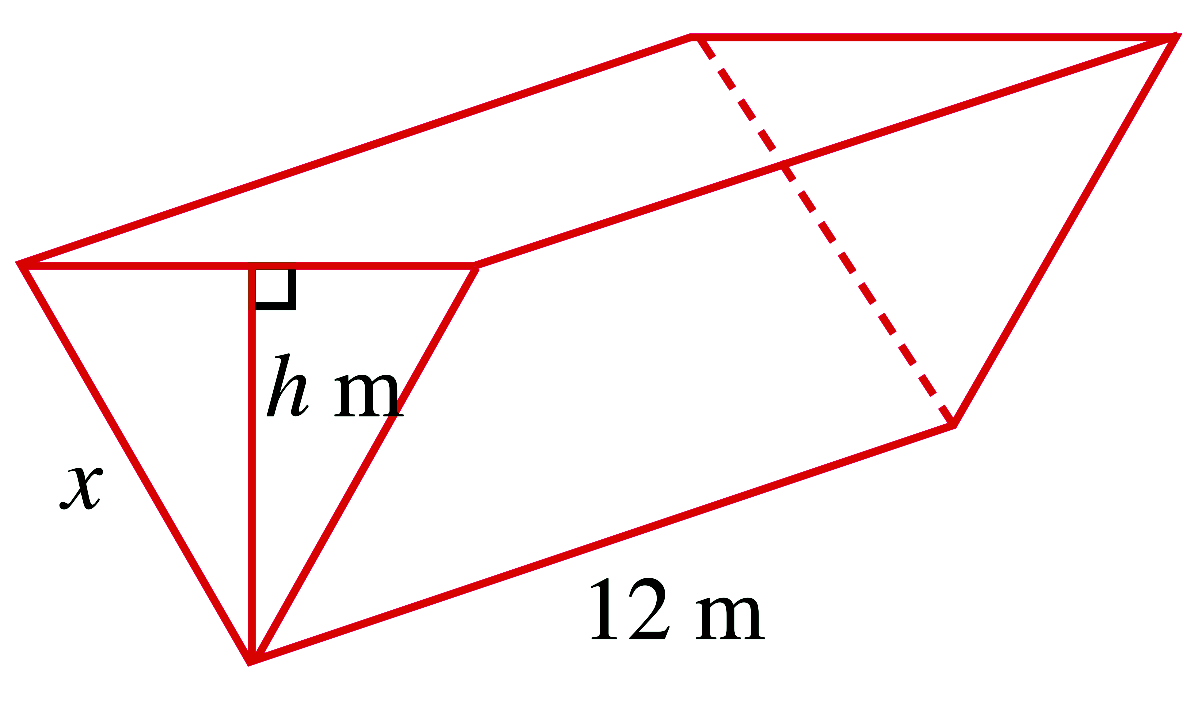
A water trough of length $12 \mathrm{~m}$ has a vertical cross-section in the shape of an
equilateral triangle of sides $x \mathrm{~m}$ and height $h \mathrm{~m}$. Express $V$, the
volume of water that the trough can hold in terms of $h$. When the height of water in the
trough is $1.8 \mathrm{~m}$, its depth is decreasing at a rate of $0.2 \mathrm{~m} / \mathrm{s}$.
Find the rate of change in the volume of water in the trough at this instant.
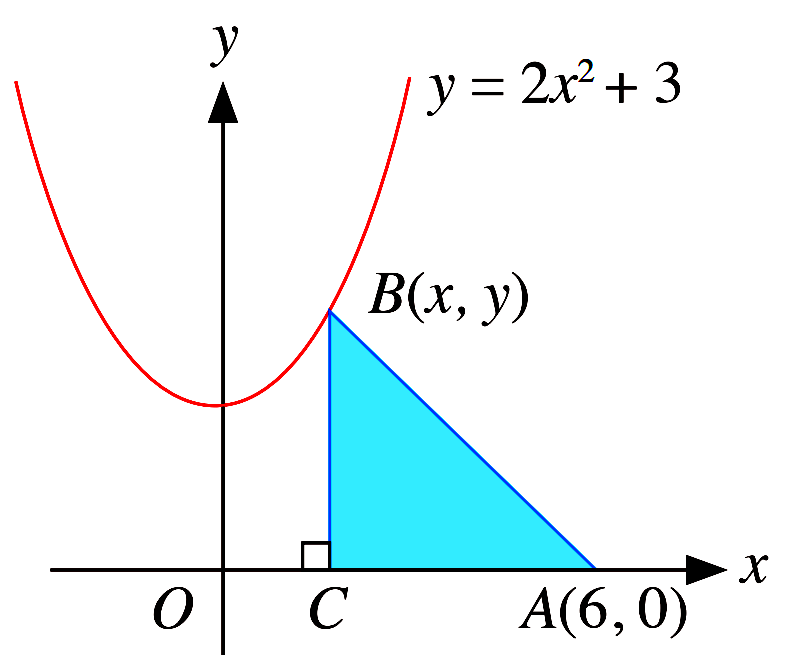
The figure shows part of the curve $y=2 x^{2}+3$. The point $B(x, y)$ is a variable point
that moves along the curve for $0 < x <6$. $C$ is a point on the $x$-axis such that $B C$ is
parallel to the $y$-axis and $A(6,0)$ lies on the $x$-axis. Express the area of the triangle
$A B C, S \mathrm{~cm}^{2}$, in terms of $x$, and find an expression for
$\dfrac{dS}{dx} .$ Given that when $x=2$, $S$ is
increasing at the rate of $0.8 \mathrm{~unit}^{2} / \mathrm{s}$, find the corresponding
rate of change of $x$ at this instant.
solution
$\begin{aligned}
\text{(a) }\quad & \frac{d}{d x}\left(2 x^{2}+3 x\right)^{10}\\\\
=& \ 10\left(2 x^{2}+3 x\right)^{9} \frac{d}{d x}\left(2 x^{2}+3 x\right)\\\\
=& \ 10(4 x+3)\left(2 x^{2}+3 x\right)^{9}\\\\
\text{(b) } \quad & \frac{d}{d x}\left(\frac{1}{3-2 x}\right)\\\\
=& \frac{d}{d x}(3-2 x)^{-1}\\\\
=& -1(3-2 x)^{-2} \frac{d}{d x}(3-2 x)\\\\
=& \frac{2}{(3-2 x)^{2}}\\\\
\text{(c) } \quad & \frac{d}{d x} \sqrt{9-x^{2}}\\\\
=& \frac{1}{2 \sqrt{9-x^{2}}} \frac{d}{d x}\left(9-x^{2}\right)\\\\
=& -\frac{x}{\sqrt{9-x^{2}}}\\\\
\text{(d) } \quad & \frac{d}{d x}\left(x^{2}+\frac{3}{x}\right)^{5}\\\\
=& 5\left(x^{2}+\frac{3}{x}\right)^{4} \frac{d}{d x}\left(x^{2}+\frac{3}{x}\right)\\\\
=& 5\left(x^{2}+\frac{3}{x}\right)^{4}\left(2 x-\frac{3}{x^{2}}\right)
\end{aligned}$
solution>
$\begin{aligned}
&\frac{d}{d x}\left[\sqrt{x+7}\left(x^{2}+2\right)^{7}\right] \\\\
=&\ \sqrt{x+7} \frac{d}{d x}\left(x^{2}+2\right)^{7}+\left(x^{2}+2\right)^{7} \frac{d}{d x} \sqrt{x+7} \\\\
=&\ 7\left(x^{2}+2\right)^{6} \sqrt{x+7} \frac{d}{d x}\left(x^{2}+2\right)+\frac{\left(x^{2}+2\right)^{7}}{2 \sqrt{x+7}} \frac{d}{d x}(x+7) \\\\
=&\ 14 x\left(x^{2}+2\right)^{6} \sqrt{x+7}+\frac{\left(x^{2}+2\right)^{7}}{2 \sqrt{x+7}}
\end{aligned}$
solution
$\begin{aligned}
& \frac{d}{d x}\left[\frac{x^{2}}{\sqrt{x+1}}\right] \\\\
=&\ \frac{\sqrt{x+1} \frac{d}{d x}\left(x^{2}\right)-x^{2} \frac{d}{d x} \sqrt{x+1}}{x+1} \\\\
=&\ \frac{2 x \sqrt{x+1}-\frac{x^{2}}{\sqrt{x+1}}}{x+1} \\\\
=&\ \frac{2 x^{2}+2 x-x^{2}}{(x+1) \sqrt{x+1}} \\\\
=&\ \frac{x^{2}+2 x}{(x+1)^{\frac{3}{2}}}
\end{aligned}$
solution
$\begin{aligned}
\text { (a) }\quad &\dfrac{d}{d x}\left[\left(2 x^{2}+3\right)^{4}\left(x^{2}-3 x\right)^{5}\right] \\\\
=&\ \left(2 x^{2}+3\right)^{4} \dfrac{d}{d x}\left(x^{2}-3 x\right)^{5}+\left(x^{2}-3 x\right)^{5} \dfrac{d}{d x}\left(2 x^{2}+3\right)^{4} \\\\
=&\ 5\left(x^{2}-3 x\right)^{4}\left(2 x^{2}+3\right)^{4} \dfrac{d}{d x}\left(x^{2}-3 x\right)+4\left(2 x^{2}+3\right)^{3}\left(x^{2}-3 x\right)^{5} \dfrac{d}{d x}\left(2 x^{2}+3\right) \\\\
=&\ 3\left(2 x^{2}+3\right)^{3}\left(x^{2}-3 x\right)^{4}\left(12 x^{3}-26 x^{2}+10 x-15\right)\\\\
\text { (b) }\quad &\dfrac{d}{d x}\left[\left(3+x^{2}\right) \sqrt{3-x^{2}}\right] \\\\
=&\ \left(3+x^{2}\right) \dfrac{d}{d x} \sqrt{3-x^{2}}+\sqrt{3-x^{2}} \dfrac{d}{d x}\left(3+x^{2}\right) \\\\
=&\ \dfrac{\left(3+x^{2}\right)}{2 \sqrt{3-x^{2}}} \dfrac{d}{d x}\left(3-x^{2}\right)+2 x \sqrt{3-x^{2}} \\\\
=&\ -\dfrac{x\left(3+x^{2}\right)}{\sqrt{3-x^{2}}}+2 x \sqrt{3-x^{2}} \\\\
=&\ \dfrac{3 x\left(1-x^{2}\right)}{\sqrt{3-x^{2}}}\\\\
\text { (c) }\quad &\dfrac{d}{d x}\left[\dfrac{\sqrt{x+3}}{x+1}\right]\\\\
=&\ \dfrac{(x+1) \dfrac{d}{d x} \sqrt{x+3}-\sqrt{x+3} \dfrac{d}{d x}(x+1)}{(x+1)^{2}}\\\\
=&\ \dfrac{\dfrac{x+1}{2 \sqrt{x+3}}-\sqrt{x+3}}{(x+1)^{2}} \\\\
=&\ -\dfrac{x+5}{2(x+1)^{2} \sqrt{x+3}}\\\\
\text { (d) } \quad &\dfrac{d}{d x}\left[\dfrac{3 x-5}{2 x^{2}+7}\right]\\\\
=&\ \dfrac{\left(2 x^{2}+7\right) \dfrac{d}{d x}(3 x-5)-(3 x-5) \dfrac{d}{d x}\left(2 x^{2}+7\right)}{\left(2 x^{2}+7\right)^{2}} \\\\
=&\ \dfrac{3\left(2 x^{2}+7\right)-4 x(3 x-5)}{\left(2 x^{2}+7\right)^{2}} \\\\
=&\ \dfrac{21+20 x-6 x^{2}}{\left(2 x^{2}+7\right)^{2}} \\\\
\text { (e) } \quad & \dfrac{d}{d x}\left[\dfrac{2 x-7}{\sqrt{x+7}}\right]\\\\
=&\ \dfrac{\sqrt{x+7} \dfrac{d}{d x}(2 x-7)-(2 x-7) \dfrac{d}{d x} \sqrt{x+7}}{x+7} \\\\
=&\ \dfrac{2 \sqrt{x+7}-\dfrac{2 x-7}{\sqrt{x+7}}}{x+7} \\\\
=&\ \dfrac{21}{(x+7)^{\dfrac{3}{2}}}\\\\
\text { (e) } \quad & \dfrac{d}{d x}\left[\sqrt{\dfrac{x^{2}+1}{x^{2}-1}}\right]\\\\
=&\ \dfrac{d}{d x}\left[\dfrac{\sqrt{x^{2}+1}}{\sqrt{x^{2}-1}}\right] \\\\
=&\ \dfrac{\sqrt{x^{2}-1} \cdot \dfrac{d}{d x} \sqrt{x^{2}+1}-\sqrt{x^{2}+1} \cdot \dfrac{d}{d x} \sqrt{x^{2}-1}}{x^{2}-1} \\\\
=&\ \dfrac{\dfrac{\sqrt{x^{2}-1}}{2 \sqrt{x^{2}+1}} \cdot \dfrac{d}{d x}\left(x^{2}+1\right)-\dfrac{\sqrt{x^{2}+1}}{2 \sqrt{x^{2}-1}} \cdot \dfrac{d}{d x}\left(x^{2}-1\right)}{x^{2}-1}=\dfrac{2 x}{\left(1-x^{2}\right) \sqrt{x^{4}-1}} \\\\
=&\ \dfrac{\dfrac{x \sqrt{x^{2}-1}}{\sqrt{x^{2}+1}}-\dfrac{x \sqrt{x^{2}+1}}{\sqrt{x^{2}-1}}}{x^{2}-1}\\\\
=&\ \dfrac{-2 x}{\left(x^{2}-1\right) \sqrt{x^{4}-1}}=\dfrac{2 x}{\left(1-x^{2}\right)}
\end{aligned}$
solution
$\begin{aligned}
\text { Curve: } y &=\frac{3 x^{2}-8}{5-2 x} \\\\
\frac{d y}{d x} &=\frac{(5-2 x)(6 x)-\left(3 x^{2}-8\right)(-2)}{(5-2 x)^{2}} \\\\
\left.\frac{d y}{d x}\right|_{(2,4)} &=\frac{(5-4)(12)+2(12-8)}{(5-4)^{2}} \\\\
&=20\\\\
\end{aligned}$
$\therefore$ The gradient of the curve $y=\dfrac{3 x^{2}-8}{5-2 x}$ at the point $(2,4)$ is 20 .
solution
Curve: $y=x \sqrt{x+3}$
$\begin{aligned}
&\\
&\frac{d y}{d x}=\frac{x}{2 \sqrt{x+3}}+\sqrt{x+3}\\\\
\end{aligned}$
When the gradient of the curve is zero,
$\begin{aligned}
&\\
&\frac{x}{2 \sqrt{x+3}}+\sqrt{x+3}=0 \\\\
&\therefore 2(x+3)=-x \Rightarrow x=-2 \\\\
&\therefore \text { When } x=-2, y=-2 \sqrt{-2+3}=-2\\\\
\end{aligned}$
The coordinate of the point at which the gradient of the curve is zero is $(-2,-2)$.
solution
$\begin{aligned}
\text { Curve: } y &=\frac{x^{2}+1}{x-1} \\\\
\text { When } x &=2, y=5 \\\\
\text { Let }\left(x_{1}, y_{1}\right) &=(2,5) \\\\
\frac{d y}{d x} &=\frac{2 x(x-1)-\left(x^{2}+1\right)}{(x-1)^{2}} \\\\
&=\frac{x^{2}-2 x-1}{(x-1)^{2}} \\\\
\therefore m &=\frac{d y}{d x} \\\\
&=-1
\end{aligned}$
The equation of normal at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
y-y_{1} &=-\frac{1}{m}\left(x-x_{1}\right) \\\\
y-5 &=1(x-2) \\\\
y &=x+3
\end{aligned}$
solution
$\begin{aligned}
\text { Curve: } y &=\frac{4 x+1}{x-1} \\\\
\text { When } y &=5, \\\\
\frac{4 x+1}{x-1} &=5 \\\\
\therefore x &=6 \\\\
\text { Let }\left(x_{1}, y_{1}\right) &=(6,5) \\\\
\frac{d y}{d x} &=\frac{4(x-1)-(4 x+1)}{(x-1)^{2}} \\\\
&=\frac{-5}{(x-1)^{2}} \\\\
\left.\frac{d y}{d x}\right|_{(6,5)} &=-\frac{1}{5}\\\\
\end{aligned}$
The equation of normal at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1} &=-\frac{1}{m}\left(x-x_{1}\right) \\\\
y-5 &=5(x-6) \\\\
5 x-y &=25
\end{aligned}$
solution
$\begin{aligned}
f(x) &=\frac{k+x}{1-2 x} \\\\
f^{\prime}(x) &=\frac{(1-2 x) \frac{d}{d x}(k+x)-(k+x) \frac{d}{d x}(1-2 x)}{(1-2 x)^{2}} \\\\
&=\frac{(1-2 x)-(k+x)(-2)}{(1-2 x)^{2}} \\\\
\therefore\ f^{\prime}(x) &=\frac{1+2 k}{(1-2 x)^{2}} \\\\
\text { Since } f^{\prime}(3) &=0.52, \\\\
\frac{1+2 k}{(1-6)^{2}} &=0.52 \\\\
\frac{1+2 k}{25} &=0.52 \\\\
1+2 k &=13 \\\\
\therefore\ k &=6
\end{aligned}$
solution
$\begin{aligned}
\text{ Curve }: y&=6-(x-2)^{4}\\\\
\text{ When } x&=1, y=5\\\\
\text{ Let } \left(x_{1}, y_{1}\right)&=(1,5)\\\\
\frac{d y}{d x} &=-4(x-2)^{3} \\\\
\therefore\ m &=\left.\frac{d y}{d x}\right|_{(1,5)} \\\\
&=4\\\\
\end{aligned}$
The equation of normal at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1} &=-\frac{1}{m}\left(x-x_{1}\right) \\\\
y-5 &=-\frac{1}{4}(x-1) \\\\
x+4 y &=21
\end{aligned}$
solution
$\begin{aligned}
\text { Curve: } y &= \left(\frac{x}{2}-1\right)^{6} \\\\
\text { When } x &= 4 \\\\
y &= \left(\frac{4}{2}-1\right)^{6} \\\\
&= 1 \\\\
\text { Let }\left(x_{1}, y_{1}\right) &= (4,1) \\\\
\frac{d y}{d x} &= 6\left(\frac{x}{2}-1\right)^{5} \cdot \frac{1}{2} \\\\
&= 3\left(\frac{x}{2}-1\right)^{5} \\\\
m &= \left.\frac{d y}{d x}\right|_{(4,1)} \\\\
&= 3\left(\frac{4}{2}-1\right)^{5} \\\\
&= 3\\\\
\end{aligned}$
$\therefore$ The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1} &=m\left(x-x_{1}\right) \\\\
y-1 &=3(x-4) \\\\
y &=3 x-11\\\\
\end{aligned}$
When this tangent meets $y$-axis, $x=0$ that implies $y=-11\\\\ $.
$\therefore$ The point $A$ is $(0,-11)$.
solution
$\begin{aligned}
\text { Curve : } y &=(x+2 a)^{3} \\\\
\text { When } y &=a^{3}, \\\\
(x+2 a)^{3} &=a^{3} \\\\
x+2 a &=a \\\\
x &=-a\\\\
\end{aligned}$
$\therefore\left(-a, a^{3}\right)$ is the point on the curve
where the tangent exists.
$\begin{aligned}
&\\
\frac{d y}{d x} &=\frac{d}{d x}(x+2 a)^{3} \\\\
&=3(x+2 a)^{2} \frac{d}{d x}(x+2 a) \\\\
&=3(x+2 a)^{2}(1) \\\\
&=3(x+2 a)^{2}\\\\
\end{aligned}$
The gradient of the tangent at $\left(-a, a^{3}\right)$ on the curve is
$\begin{aligned}
&\\
m &=\left.\frac{d y}{d x}\right|_{\left(-a, a^{3}\right)} \\\\
&=3(-a+2 a)^{2} \\\\
&=3 a^{2}\\\\
\end{aligned}$
$\therefore$ The equation of tangent at $\left(-a, a^{3}\right)$ is
$\begin{aligned}
&\\
y-a^{3} &=m(x-(-a)) \\\\
y-a^{3} &=3 a^{2}(x-(-a)) \\\\
y &=3 a^{2} x+4 a^{3}
\end{aligned}$
solution
$\begin{aligned}
\text{Curve }: y&= \frac{x+1}{x-1}\\\\
\frac{d y}{d x}&= \frac{(x-1)-(x+1)}{(x-1)^{2}}\\\\
&= -\frac{2}{(x-1)^{2}}\\\\
\text{Line }: 2 y+x&= 6 \\\\
y&= -\frac{1}{2} x+3\\\\
\end{aligned}$
Since the tangents are parallel to the given line,
$\begin{aligned}
&\\
-\frac{2}{(x-1)^{2}}&= -\frac{1}{2}\\\\
(x-1)^{2}&= 4\\\\
x-1&= \pm 2 \\\\
x&= -1 or x= 3 \\\\
\text{ When } x&= -1, y= 0 \\\\
\text{ When } x&= 3, y= 2\\\\
\end{aligned}$
Let $\left(x_{1}, y_{1}\right)= (-1,0)$ and $\left(x_{2}, y_{2}\right)= (3,2)\\\\ $
$\therefore$ The equation of tangent at $\left(x_{1}, y_{1}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&= m\left(x-x_{1}\right)\\\\
y-0&= -\frac{1}{2}(x+1) \\\\
x+2 y&= -1
\end{aligned}$
$\therefore$ The equation of tangent at $\left(x_{2}, y_{2}\right)$ is
$\begin{aligned}
&\\
y-y_{1}&= m\left(x-x_{1}\right) \\\\
y-2&= -\frac{1}{2}(x-3) \\\\
x+2 y&= 7
\end{aligned}$
solution
$\begin{aligned}
y &=\frac{x^{2}+6}{x-3} \\\\
\frac{d y}{d x} &=\frac{(x-3)(2 x)-\left(x^{2}+6\right)(1)}{(x-3)^{2}} \\\\
&=\frac{2 x^{2}-6 x-x^{2}-6}{(x-3)^{2}} \\\\
&=\frac{x^{2}-6 x-6}{(x-3)^{2}}\\\\
\text{ When } x&=4,\\\\
\frac{d y}{d x} &=\frac{4^{2}-6(4)-6}{(4-3)^{2}} \\\\
&=-14\\\\
\therefore\ \text{ Gradient of tomegent } &=-14\\\\
\therefore\ \text{ Gradient of normal } &=\frac{1}{14}\\\\
\text{ When } x&=4,\\\\
y&=\frac{4^{2}+6}{4-3}\\\\
&=22
\end{aligned}$
solution
$\begin{aligned}
h &=\dfrac{\sqrt{3}}{2} x \\\\
x &=\dfrac{2}{\sqrt{3}} h \\\\
\text { area of cross-section } &=\dfrac{1}{2} x h \\\\
&=\dfrac{1}{2} \cdot \dfrac{2}{\sqrt{3}} h \cdot h \\\\
&=\dfrac{h^{2}}{\sqrt{3}} \\\\
\text { volume of trough } &=V \\\\
\therefore V &=\dfrac{12 h^{2}}{\sqrt{3}} \\\\
&=\dfrac{4 \sqrt{3}}{3} h^{2} \mathrm{~m}^{3} \\\\
\text { When } h &=1.8 \mathrm{~m}, \\\\
\dfrac{d h}{d t} &=0.2 \mathrm{~m} / \mathrm{s}\\\\
\text { Since } V &=\dfrac{4 \sqrt{3}}{3} h^{2}, \\\\
\dfrac{d V}{d h} &=\dfrac{2 \sqrt{3}}{3} h \\\\
\text { When } h &=1.8 \mathrm{~m} \\\\
\dfrac{d V}{d h} &=\dfrac{2 \sqrt{3}}{3}(1.8) \\\\
&=2.08 \\\\
\dfrac{d V}{d t} &=\dfrac{d V}{d h} \cdot \dfrac{d h}{d t} \\\\
&=2.08 \times 0.2 \\\\
&=0.416 \mathrm{~m}^{3} / \mathrm{s}
\end{aligned}$
solution
$\begin{aligned}
\text { Curve: } y &=2 x^{2}+3 \\\\
\therefore \frac{d y}{d x} &=4 x \\\\
\text { Area of } \triangle A B C &=\frac{1}{2} A C \cdot B C \\\\
S &=\frac{1}{2}(6-x)(y) \\\\
S &=\frac{1}{2}(6-x)\left(2 x^{2}+3\right) \\\\
&=\frac{1}{2}\left(-2 x^{3}+6 x^{2}-3 x+18\right) \\\\
\frac{d S}{d x} &=\frac{1}{2}\left(-6 x^{2}+12 x-3\right) \\\\
&=-\frac{3}{2}\left(2 x^{2}-6 x+1\right)\\\\
\text { When } x&=2,\\\\
\frac{d S}{d x} &=-\frac{3}{2}(8-12+1) \\\\
&=\frac{9}{2} \\\\
\frac{d S}{d t} &=0.08 \text { unit / s}\quad \text { (given) } \\\\
\frac{d S}{d t} &=\frac{d S}{d x} \cdot \frac{d x}{d t} \\\\
0.08 &=\frac{9}{2} \cdot \frac{d x}{d t} \\\\
\frac{d x}{d t} &=\frac{0.16}{9} \\\\
&=0.018 \text { unit/s }
\end{aligned}$


Posting Komentar untuk "Calculus Exercise (5) : Change Rule, Product Rule and Quotient Rule"